<-CHM151 Home Page
ELECTRON CONFIGURATION Tutorial and Quiz
Last update (7/29/10)
 |
In the last tutorial, I already introduced you to quantum numbers which define the size, shape, orientation, and spin of electrons. Since that tutorial was already information overload, I didn't go into how this progression is represented. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
Like I said before, learning chemistry is like being a symbologist. Symbols is your specialty. Just take pride in it and then learning doesn't hurt so much. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
As you know, all areas of chemistry can be broken down into these 3 areas of focus. In learning about electron configuration, the building blocks are simply electrons with some mention of protons. Force and energy are also considered in understanding how the electrons choose their configuration. Mathematics in this topic is on two extremes. First graders can do most of it because it's like counting to 14. Then there's the theory behind it that's way behind this course. Let's do a quick review. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
This is the electron of hydrogen. We often show it as a particle, a wave, or electron cloud. Roll cursor over image to see the transformation.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
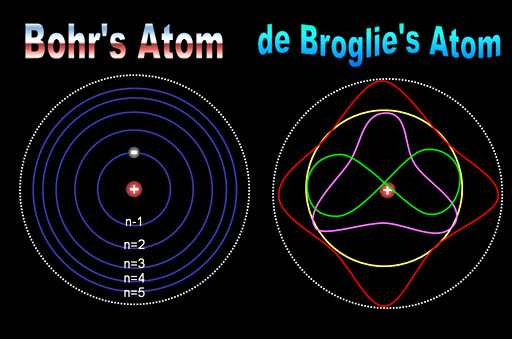 |
Bohr’s atom showed electrons as particles similar to planets going around the sun. de Broglie’s atom treats electrons more as waves with wave patterns that fit symmetrically within the atom. In both cases, the energy levels of the electrons must go up by an incremental quantity (quantum). Both of these played a role in the modern theory of the atom and the structure of the electrons. As elements were built by adding one proton and one electron at a time, the electrons would find a position and shape that maximized their distance from each other (from repulsion) yet kept them as close as possible to the positive nucleus (attraction). The way they positioned themselves followed a fairly basic pattern known as its quantum number. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
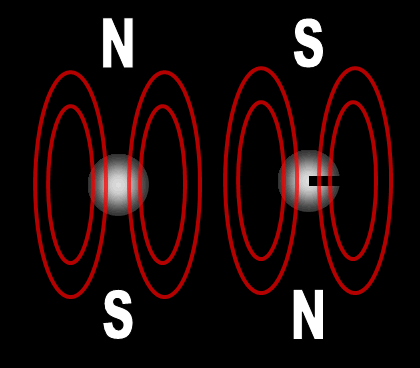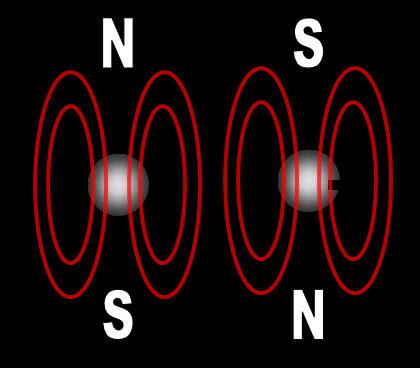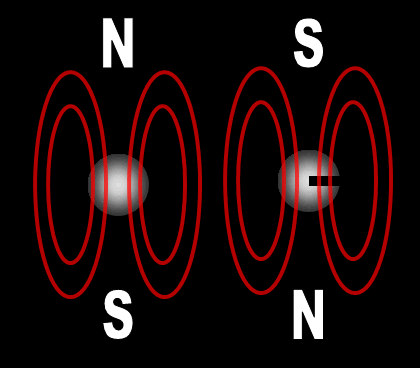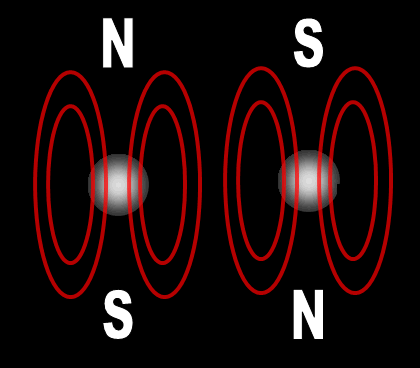 |
Each electron has their own unique 4 quantum numbers represented by n, l, m, and s. This is known as the Pauli Exclusion Principle named after Wolfgang Pauli and his statement that electrons are excluded from having the same quantum numbers. In other words, they can't be in the same place at the same time with one exception. If their spins are opposite, they can. A spinning charge produces a magnetic field. If they spin in opposite directions, then the north and south poles will align and they will attract each other (opposites poles attract). At least this is one way the spin of electrons is visualized. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
Sometimes these quantum numbers are represented as n, l, ml, and ms, but here we will just use n, l, m, and s. The n is called the principle quantum number. It's often referred to as the shell number because in Bohr's atom, each increasing orbit forms a shell around the inner ones. In the past, these shells were called K, L, M, N, and O. Those correspond to n=1, 2, 3, 4, & 5. You may still see reference to these letters in the literature. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
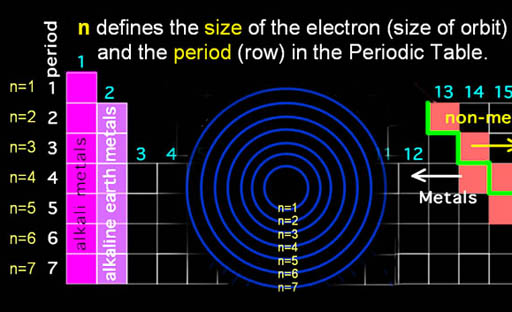 |
Also, "n" corresponds to the row (or period) on the Periodic Table. By the way, the first elements in the left two columns have outer electrons in the s orbital. Note, this "s" is a name of an orbital, not the "s" in "n, l, m, s" where that "s" refers to the spin of an electron. There are only 27 letters in the alphabet, but in chemistry and physics they may represent over a hundred different things. So we will see the same letter used to mean different things.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
This is the hydrogen atom with its one electron in its ground state (lowest energy). The "1" in front of "1s1" means this is n=1. The "1" exponent means there's just "1" electron in that orbital. The "↑" indicates a +½ spin. Whether electrons actually spin is debated but it's one property of electron's configuration. When n=1, then l and m quantum numbers can only be zero. If the electron was boosted to the second shell (n=2), then the arrow below would be in the 2s box.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
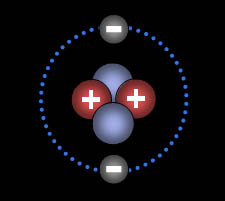 |
This is the helium atom. It has 2 electrons. These are able to share the same s orbital because of opposite spins. The "2" in "1s2" means there are 2 electrons in that orbital. "s" orbitals can only hold 2 electrons, so that's as high as you will ever see it. The 1 in "1s2" means this is the s orbital belonging to the n=1 shell.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
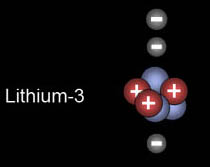 |
This is lithium. The third electron is in shell n=2.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
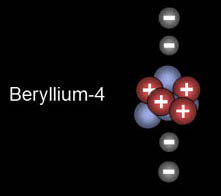 |
This is beryllium. The fourth electron completes the 2s orbital. Again, it has to have opposite spin.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
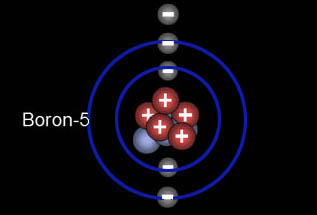
This is boron. The 2s orbital is full, so the expansion begins in the 2p orbital. "2p" means this orbital belongs to the n=2 shell. The fifth electron is the first p orbital electron. It is drawn as a particle in the upper image but actually has the dumb bell shape of a p orbital shown in the lower image. Notice the first p orbital occurs when the l quantum number is 1. So when you hear l=1, think p orbital. Also, note, that l starts at 0, and then counts up to n-1. Since this n=2 row, l started as l=0 for the s orbital and can only go up to l=1 (one less than the n value). The 3 boxes for the 2p orbital are called subshells of the p orbital.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
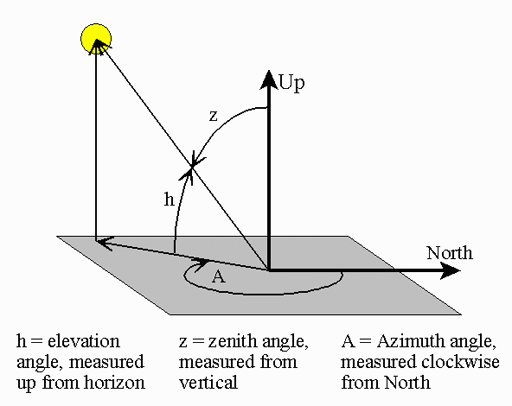 |
Note: The l quantum number is a lower case "L" that is italicized. The letter "l" and number "1" look alike but remember they are different. There are 3 names for the l quantum number: azimuthal, angular, and orbital. The word "azimuthal" comes from "azimuth" which is from Arabic "as sumut" meaning "the way" or "the direction". It is used in astronomy and gunnery to indicate the clockwise angle from North. In the image the azimuth angle is about 200°. So we see why it is also called the angular quantum number. It indicates a rotational motion of the wave. It's also called the orbital quantum number because it is this l quantum number that determines the kind of orbital (shape of the electron). This is important because the different types of orbitals (different l numbers) have different strengths in chemical bonding. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
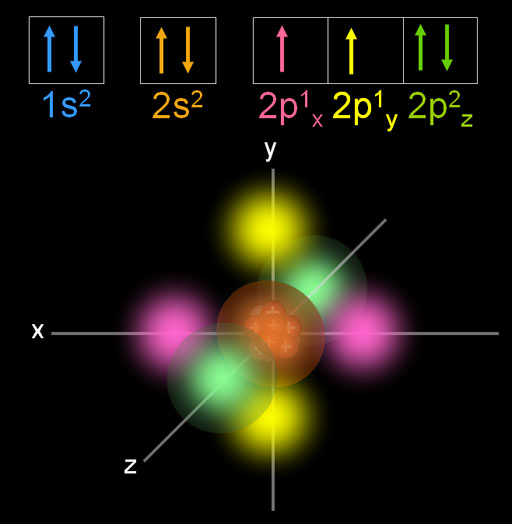
This is carbon. It is adds another electron to the p orbital. This time I'm showing the electron cloud of the p orbitals. Notice the x, y, and z axes. The first 3 p orbital electrons will align with each axis. Carbon only has 2 p orbital electrons. I put the first one (pink) on the x axis and the second one (yellow) on the y axis. They don't share the same space by having opposite spins because that takes more energy than filling up an empty p orbital. Changing orientation keeps the electrons farther apart. The different orientations are indicated with the m quantum number. This is also called the magnetic quantum number. Notice the m quantum number starts with the negative of the l quantum number. Since we are at the l=1 quantum number (p orbital), the m quantum numbers start out as -1, then go up to 0 on the next electron, and +1 on the third electron. Each time it changes its orientation along a different axis. The three m quantum numbers make up the three subshells of the p orbital.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
This is oxygen. We skipped nitrogen, but nitrogen added one electron to the z axis of the p orbital. Oxygen has 8 protons and 8 electrons. The first 4 are in the first 2s orbitals. The last electron was forced to share one of the p orbitals with an existing electron. I put it with the one on the z axis, but they are all the same. Notice the m quantum number increased to +1 for the 3rd and 4th electrons aligning them with the z axis. However, they must have opposite spins to share that same space. By the way, the 2 unpaired electrons in m=0 and m=+1 orientations are responsible for the magnetic properties of oxygen.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
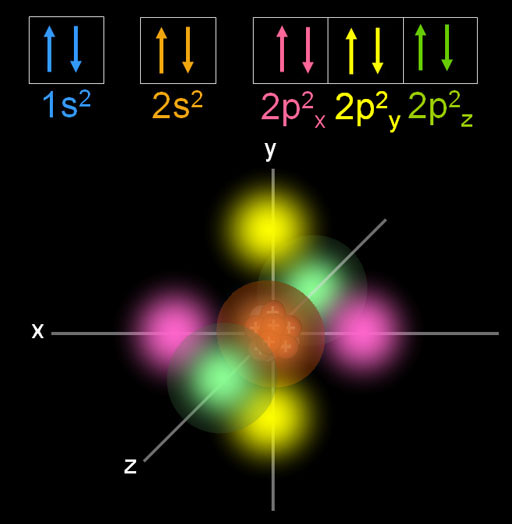 |
This is neon. We skipped fluorine, which added one more electron to fill 2p2y. At neon all of the p orbitals are filled. It has 3 orientations (x, y, and z) that are filled with 2 electrons each. This is a very stable configuration for the 8 electrons in the 2s and 2p orbitals. You may know it as the famous octet that many elements try to reach. So we see all of these p orbital electrons have the same n=2 principal quantum number and the same l=1 angular quantum number (l=1 has dumb bell shape and is called the p orbital). Pairs of electrons with opposite spins (+1/2 & -1/2) are aligned along x, y, and z axes indicated by the m=-1, m=0, and m=-1 magnetic quantum numbers.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
After all of these symbols, test your knowledge. Match the left symbol with the one best match on the right.
Answers are at the very bottom of this page.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Practice Problem 8: How many electrons are in this element that has this electron configuration? Practice Problem 9: How many electrons are needed for this element to complete the octet in shell 2 (n=2)? Practice Problem 10: What is this element? |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
After the 2p electron orbital is filled, the elements start filling the 3s orbital. The filling is just like it did in row 2. So if you look at rows 2 and 3 on the Periodic Table, you will see they look the same. In other words, 2 electrons fill the s orbital and 6 electrons fill the p orbital. The only difference in the quantum numbers is the n=3, which is reflected in the electron configuration notation as 3s23p6. Note: I left off the "s=" below to save space. The spins of +½ and -½ are obvious.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
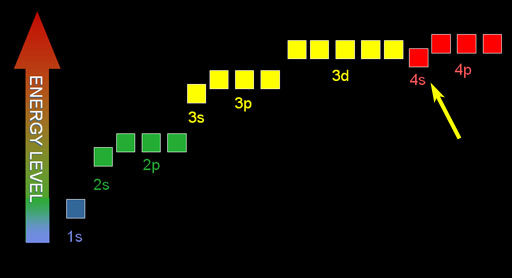 |
According to quantum theory, the angular (orbital) number represented by "l" counts up to one less than the principle quantum number of n. For example, if n=3, then "l" would go 0, 1, 2. Therefore, for n=3, l=0 is3s orbital, l=1 is 3p orbital, and l=2 is 3d orbital. In the image on the left, we can see the energy levels of this progression goes up. However, because the energy levels of 4s orbital electrons are lower than the 3d electrons, they get filled before the 3d electrons. Look at the Periodic Table above. The first two columns for row 4 are the elements where the 4s electrons are being filled. The yellow block of 10 elements that follow are the ten 3d electrons that are filled after the 4s electrons. So the order of electron filling is from lowest energy to higher energy. This is called the Aufbau principle named after the German word that means "building up." In other words, the general pattern of electron filling is guided by the counting up of the quantum numbers. (n=1: l=0, m=0) (n=2: l=0, m=0 → l=1, m=-1, 0, 1) (n=3: l=0, m=0 → l=1, m=-1 ,0, 1 → l=2, m=-2, -1, 0, 1, 2) (n=4: l=0, m=0 → l=1, m=-1 ,0, 1 → l=2, m=-2, -1, 0, 1, 2 → l=3, m=-3, -2, -1, 0, 1, 2, 3 ) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
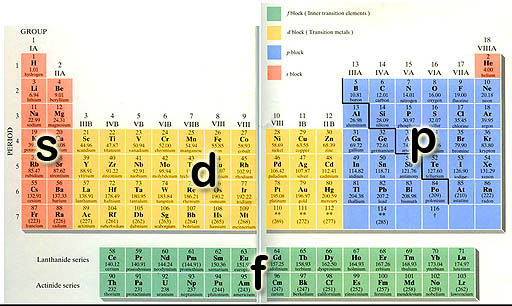 |
The above progress is modified to let electrons orbitals that have the lowest energy fill first. The first instance of that (as mentioned) is when the 4s electrons fill before the 3d electrons. This also happens when 5s electrons fill before 4d electrons (Period 5). On row 6 (period 6) the two 6s electrons are filled followed by the first 5d electron for element 57 (Lanthanum). But then the 4f electrons start filling. That's the first green row you see at the bottom. That starts with element 58. On some Periodic Tables element 57 (Lanthanum) is included on the bottom row. They call this the lanthanum series. That is the series of elements where the f orbital electrons start to get filled. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Below is progression up through the transition metals that is the d block on the Periodic Table (image on left above). The last element that has all of these electrons is zinc. It's electron configuration would be written as 1s22s22p63s23p64s23d10. As you can see it gets a bit long. To shorten it they usually use the element symbol of the noble gas that came before the element. Argon has the electron configuration of 1s22s22p63s23p6, so for zinc, it's OK to write [Ar]4s23d10. The [Ar] means the inner electrons have the same electron configuration as argon. Then on top of the inner electrons are two 4s electrons and ten 3d electrons filling the five 3d subshells (five m orientations)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
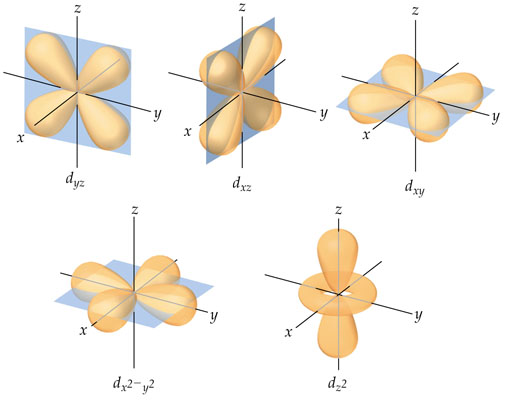 |
Recall the magnetic quantum number (m) dictates an orientation of the electron. In the above chart I used yz, xz, xy, etc. for the d orbital electrons. The image on the left shows these orientations. Again, the whole purpose is to give electrons more space between them because of the repulsion. The wave shape of the five d electrons on the left is bit more complex than those of the s and p orbitals. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Below is the electron configuration up to krypton. Again, the filling of the 3d orbital interrupts the filling of the 4p orbital. The pattern below repeats itself for the n=5 shell. Then on the n=6 shell (row 6), there's an interruption of the filling of the d orbitals by f orbitals. The reason, as usual, is they have lower energy levels.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Below is the entire Periodic Table which shows the electronic configuration for all elements. This was tough to create, but I got it done. The progression is pretty consistent except for a few exceptions. For example, look at chromium (group 6, period 4) and copper (group 11, period 4). Chromium shows 4s13d5. Instead of having 2 electrons in the 4s2 and 4 electrons filling the first 4 electrons in 3d orbital (3d4) as predicted, it took an electron from 4s2 which leaves it as 4s1 and filled the first 5 electrons in 3d orbital (3d5). There still are just 6 electrons (group 6) but they are not split 2 in the 4s orbital and 4 in the 3d orbital. The 4s13d5 means 1 is in the 4s orbital and 5 are in the 3d orbital. So every once in awhile, you will see these anomalies. It's not fully understood why this happens, but it's probably because that arrangement is more stable (has lower energy).
The purpose of learning these electron configurations is to know what electrons are available for bonding. This gives you insight in how elements will bond. In the next chapter when you learn more about bonding, you will see the usefulness of these electron configurations. Practice Problem 11: Which orbital is being filled in the alkali metal column? |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Answers to Practice Problems: 1=c, 2=a, 3=c, 4=a or d, 5=a, 6=d, 7=b, 8=7 electrons, 9=3 electrons needed, 10=nitrogen, 11=s orbital, 12= 1s22s22p63s23p5, 13=5p1 electron would be given up,. 14= 5p1, and both electrons in 5s2 would be given up, 15=it loses the 3p1 and the 3s2 electrons. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||