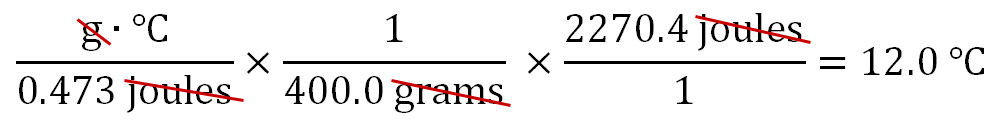You may remember from the metrics tutorial that distance, mass, and volume were based on water. The same is true with some units of energy. This liter bottle will help illustrate these units. If you took the bottle and threw it so while the bottle was in your hand it traveled one meter and the bottle was going 1 meter per second speed as you let it go, one "joule" of energy was transferred to the bottle. (Joule is named after James Joule) The force that you exerted on the the kilogram of water to get that liter of water up to 1 meter per second is defined as one "newton" of force (Symbol is N). Energy is often calculated as force times distance. So in this case, one newton of force times one meter is called either newton·meter or one joule.



Another unit of energy based on water is the calorie. A calorie is defined as the amount of energy needed to raise 1 gram of water 1 degree Celsius. If it is a kilogram of water (1 liter), they call that a kilocalorie or a food calorie.
In this example. we have a kilogram of water. That would take 1,000 calories to raise it 1 degree Celsius. If going from room temperature (20°C) up to near boiling (90°C), that's a 70 degree increase and therefore 70 x 1000 calories, or 70,000 calories to heat it.



A
|
B |
C |
D |
E |
F |
G |
H |
I |
J |
|
| 1 | ||||||||||
| 2 | 1 |
kilowatt·hour | 1 |
joule/sec | 1000 | 3600 |
sec | = |
3600000 |
joules |
| 3 | 1 |
watt | kilo | 1 |
hour |


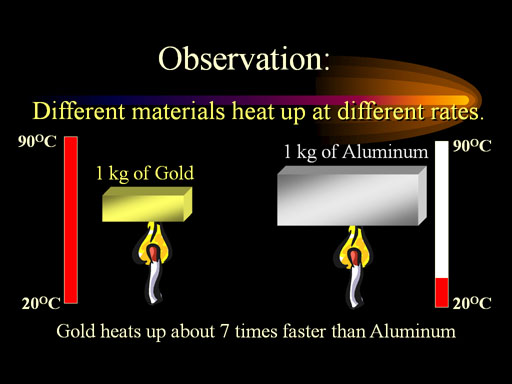
For example, the specific heat of gold is over 30 times smaller than that of water. In other words, a kilogram of gold will go from 20°C to 90°C, while water will only go from 20°C to 22°C when they both are heated equally. The specific heat of gold is 0.031 calories per gram per degree Celsius (0.031cal/g·°C).
Why such a big difference? (See next paragraph(



A more common approach to find the specific heat of a substance (like metals) is to heat that substance and then put it into a known amount of water.
The blacksmith may have been one of the first people to recognize this. They often drop various metals into a bucket of water to cool the metal. They undoubtedly noticed that the water would heat up. They knew the heavier the piece of metal, the more the water would heat up. They may have noticed that different metals of equal weight would not heat up the water to the same temperature.

As we would suspect a hot iron horseshoe dropped into this water will heat up the water at the same time as cooling off the horseshoe. Also, in a minute or so, the horseshoe and water will be the same temperature.
By knowing the mass of the horseshoe, the mass of the water, plus the beginning temperatures of the water and horseshoe, along with the final temperature of the water, we can figure out the specific heat of iron.

The trick to figuring this out is to recognize that the energy lost by the horseshoe will be the energy gained by the water. In other words the calories lost is equal to the calories gained.
Specific heat is calories per gram per degree Celsius. That means if we multiply by grams and degrees Celsius, those units cancel and we are left with just calories (energy)

Let's say this horseshoe weighed 449 grams and was 455°C before dropping into the water. There were 2.00 liters (2,000g) of water, which started out at 24°C and ended up at 34.2°C. What is the specific heat of iron?
Again, we set up an equation that shows the energy lost by the iron equals the energy gained by the water.
Notice in the spreadsheet below that the one °C in the denominator cancel both of the °C in the numerator because after those in the numerator are subtracted, there's only one °C left.
A
|
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
T |
U |
|
Energy lost from the horseshoe |
equals |
Energy gained by the water | ||||||||||||||||||
| 1 | unknown specific heat |
mass iron |
Final Temp |
Initial Temp |
specific heat water |
mass water | Final Temp |
Initial Temp |
||||||||||||
| 2 | - |
??? |
calories | 449 |
g | 34.2 |
°C | - |
455 |
°C | = |
1.00 |
calories | 2000 |
g | 34.2 |
°C | - |
24.0 |
°C |
| 3 | g·°C | g·°C | ||||||||||||||||||
| 4 | Formula in I5 is "=D2*(F2-I2)" |
Formula in L5 is "=N2*(P2-T2)" | ||||||||||||||||||
| 5 | - |
??? |
calories | x |
-188939 |
g·°C | = |
20400 |
calories | |||||||||||
| 6 | g·°C | |||||||||||||||||||
| 7 | Solving for unknown specific heat by dividing both sides by 188939 g·°C |
|||||||||||||||||||
| 8 | Formula in I8 is "=L8/L9" |
0.108 |
calories | = |
20400 |
calories | Formula in L8 is "=L5" | |||||||||||||
| 9 | g·°C | 188939 |
g·°C | Formula in L9 is "=I5" | ||||||||||||||||
Here we get the specific heat of the iron in the horseshoe as 0.108 calories per g per °C. If this is entered in a spreadsheet, you can change any of the values in row 2 and the specific heat will automatically be calculated in I8.
How many joules of energy are required to preheat a 5.0 kilogram iron skillet from 25.0°C to 150.0°C. The Specific Heat of iron is 0.452 joules/g·°C. Sometimes textbooks or instructors use the following formula to find the energy: q=mcΔT, where "q" is energy in joules; "m" is mass in grams; "c" is the Specific Heat; and ΔT is the change in temperature in Celsius. However, to use this formula, you would have to memorize it. I prefer to use dimensional analysis (set up in a spreadsheet format) to find the answer without any memorization. We know we want the answer in joules, so the calculations need to end up in joules. So after the equal sign below, we put ??? joules as the quantity we want to end up with (cells I2 and J2).
A
|
B |
C |
D |
E |
F |
G |
H |
I |
J |
|
| 1 | = |
??? |
joules | |||||||
| 2 |
Next we look at the question for any data that has the units of "joules" in it. That will help guarantee that we end up with joules. Notice the Specific Heat for iron is 0.452 joules/g·°C. So we start with that piece of data.
A
|
B |
C |
D |
E |
F |
G |
H |
I |
J |
|
| 1 | 0.452 |
joules | = |
??? |
joules | |||||
| 2 | grams·°C |
Note that spreadsheets have the number value in one cell (A1) and the units in a different cell (B1 & B2). It can't do any calculations if a number and unit is in the same cell. Since our answer is only in joules, we have to cancel out the grams and Celsius in cell B2. The only way to cancel a unit of measurement is to use the same unit of measurement. That means to get rid of grams, we need to use some other data that is measured in grams. Here we see grams in the 5.0 kilogram mass of the skillet. So we put that data in the numerator (D1) so it will cancel the grams in the denominator (cell B2). Note, the "kilo" part of kilograms is not canceled. After this multiplication the result would be in joules per degree Celsius (J/°C). So we are closer to our final answer of joules, but we still need to get rid of degrees Celsius.
A
|
B |
C |
D |
E |
F |
G |
H |
I |
J |
|
| 1 | 0.452 |
joules | 5.0 |
kilo |
= |
??? |
joules | |||
| 2 |
To get rid of degrees Celsius, we need to use some other data in the problem that has the units of Celsius. The problem says we heat it from 25.0°C to 150.0°C. The rise in temperature would be 125°C. So that has the unit of °C that we can use to cancel the °C in cell B2. So we let that be the next number that we multiply by. Again, this has to be in the numerator (F1) in order it to cancel out the °C in the denominator (cell B2).
A
|
B |
C |
D |
E |
F |
G |
H |
I |
J |
|
| 1 | 0.452 |
joules | 5.0 |
kilo |
125 |
= |
??? |
joules | ||
| 2 |
If we were to multiply these quantities, the units of grams and Celsius would be gone, but the answer would be in kilojoules because we didn't get rid of the "kilo" that was in kilograms. To get rid of "kilo", we multiply by the fraction 1000 over "kilo". Since "kilo" means 1000, multiplying by 1000 over kilo is the same as multiplying by 1000/1000 (which is 1 so it doesn't change the final answer, but it will get rid of the kilo prefix).
A
|
B |
C |
D |
E |
F |
G |
H |
I |
J |
|
| 1 | 0.452 |
joules | 5.0 |
125 |
1000 | = |
??? |
joules | ||
| 2 |
Since "kilo" means 1000, what we are basically doing in column G is replacing the word "kilo" with 1000. So "kilo" is not removed and our answer is only in joules. So the last thing to do is to multiply all of the numerators (row 1). If there were any numbers in the denominator of these fractions, you would divide by those numbers. So below is the final set up with the final answer in joules. Notice we didn't use any formulas, we just looked the unit in the answer and started from there.
A
|
B |
C |
D |
E |
F |
G |
H |
I |
J |
|
| 1 | 0.452 |
joules | 5.0 |
125 |
1000 | = |
282500 |
joules | ||
| 2 |
The calculator comes up with 282,500 joules. However, we have to remember to consider the accuracy of our data (the significant figures of each piece of data). The Specific Heat of 0.452 joules has three significant figures. The mass of 5.0 kilograms has two significant figures. The rise in temperature of 125°C has three significant figures. The 1000 for kilo is an exact number, so we don't need to worry about it. The final answer is only as accurate as the least accurate piece of data, which would be the mass (5.0 kilograms). So our final answer should also reflect that same accuracy of 2 significant figures. 282,500 has 4 significant figures (the last 2 zeros don't count). If we round the answer to 280,000 we would be correctly showing 2 significant figures. A preferred way would be to express this answer in scientific notation such as 2.8 x 105 joules, which also shows 2 significant figures (the 2 & 8). Below is what the calculations look like written as a series of fractions (usual way dimensional analysis is done). Again note all units (dimensions) get canceled except for joules. I prefer using a spreadsheet because then I get the spreadsheet to do all of the calculations.
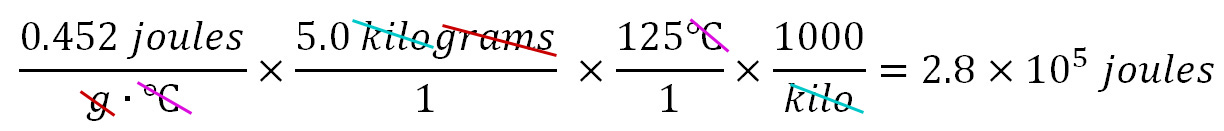
250.0 grams of a metal releases 5000 joules of energy and its temperature drop is from 90°C to 15.7°C. What is the Specific Heat of the metal? Here again we use the dimensions (units of measurement) to show us how to calculate this answer. The units of Specific Heat is joules per gram per degree Celsius (J/g·°C). So we write those units in the answer after the "=" sign. These units also show us that joules is in the numerator (top) and is divided by grams and degrees Celsius that are in the denominator (on the bottom).
A
|
B |
C |
D |
E |
F |
G |
H |
I |
|
| 1 | = |
??? |
joules | ||||||
| 2 | grams·°C |
Since we need joules in our final answer, we need to find a piece of data in the problem that uses joules. That would be the 5000 joules of energy that the metal gave off when it cooled. The final answer also has grams in it, so we need to use the grams in the problem (250.0 grams). Because grams is in the denominator, we need the 250.0 grams to also be in the denominator (so that it gets divided into the 5000 joules). The final answer also has °C in the denominator, so we also need to divide by the change in temperature (ΔT) of 74.3°C(90°C-15.7°C). Instead of canceling units like we often do; this problem needed for us to add the units of grams and °C, which we did when we divided by them.
A
|
B |
C |
D |
E |
F |
G |
H |
I |
|
| 1 | 5000 |
joules | = |
0.269 |
joules | ||||
| 2 | 250.0 |
grams | 74.3 |
°C | grams·°C |
250.0 grams has 4 significant figures and 74.3°C has three. The 5000 joules only has 1 significant figure unless there was a decimal point after the 5000 (5000.), then it would have had 4 significant figures. With only 1 significant figure, the answer would be 0.3 joules/g °C. Otherwise, the answer would have 3 sig figs (0.269 joules/g °C) because of the temperature data has three. spreadsheet to do all of the calculations. Below is what the above calculations look like using fractions. The arithmetic is easy; divide 5000 by 250, then take that answer and divide by 74.3
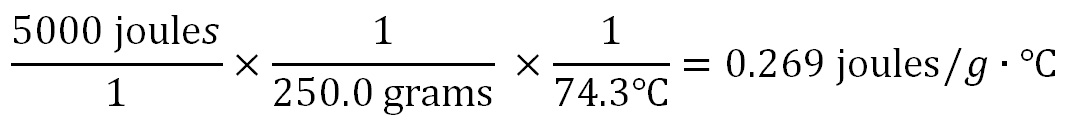
The Specific Heat of iron used is 0.473 J/g·°C. A 400.0 gram sample of iron at 20.0°C releases 2270.4 joules of heat energy. What is the new temperature of iron? This is a little different than the previous problems, because before we used the change in temperature (ΔT) in the calculations. Not just a starting or ending temperature. So we will solve for (ΔT), then afterwards, it's a simple task to find the final temperature.
A
|
B |
C |
D |
E |
F |
G |
H |
I |
|
| 1 | = |
??? |
ΔT in °C | ||||||
| 2 |
Our approach is to start the calculation with data that also has degrees Celsius in it. That guarantees our answer will have the units of degree Celsius. In this problem, we have the 20°C starting temperature and we have the Specific Heat of iron of 0.473 J/g·°C that also has degree Celsius in it. We can't use the 20°C now because we will use that after we find the change in temperature ΔT. So we need to use the Specific Heat of iron. However, in Specific Heat the °C in the denominator. We need it in the numerator (top) because our ΔT is in the numerator in the final answer (on row 1). So we invert the Specific Heat value. See below. The value and joules are in the denominator (row 2) and grams and °C are in the numerator (row 1).
A
|
B |
C |
D |
E |
F |
G |
H |
I |
|
| 1 | grams·°C | = |
0.269 |
ΔT in °C | |||||
| 2 | 0.473 |
joules |
Like before, the strategy is to get rid of the units that are not in the final answer. In this case, those are "joules" and "grams". We can use the 400.0 grams of iron to cancel out the grams in cell B1. The 400.0 grams has to be in the denominator in order for them to cancel (the one on bottom divides into the top one and the result is just "1"). To get rid of joules in B2, we use the 2270.4 joules of energy released (E1 and F1). Those have to be in the numerator in order to cancel out the joules in the denominator (cell B2). To solve the problem, any numbers in the top row (numerators) are multiplied. Here it's just 2270.4, so there's nothing to multiply it by; however, we do divide the 2270.4 by 0.473, followed by 400. The calculator says that answer is 12, which is the change in temperature in °C. We should write that as 12.0°C so that it shows 3 significant figures to match 0.473 J/g·°C, which has the fewest sig figs.
A
|
B |
C |
D |
E |
F |
G |
H |
I |
|
| 1 | 2270.4 |
= |
12.0 |
ΔT in °C | |||||
| 2 | 0.473 |
400.0 |
The change in temperature comes from subtracting the final temperature (let's use TF to represent that) from the starting temperature (20.0°C). Algebraically, that is written as:
20.0°C - TF = 12.0°C
To solve for TF, we can subtract 20.0C from both sides to get TF by itself.
20.0°C - TF - 20.0°C = 12.0°C - 20.0°C
That cancels out the 20.0°C and gets TF by itself on the left side.
- TF = -8.0°C
The only problem is that we have the negative of our answer. So by multiplying by -1 to both sides we end up with final temperature of 8.0°C.
TF = 8.0°C
So dimensional analysis found the change in temperature, and then we used some basic algebra to solve for the final temperature. Also, note that we had to invert the Specific Heat in order to get the degrees Celsius in the numerator. So this problem was a bit trickier than the previous ones. Below is the spreadsheet calculations shown in fraction format.