
11th Edition

12th Edition
 Instructions are given for the 11th, 12th, and 13th
Editions.
Instructions are given for the 11th, 12th, and 13th
Editions.
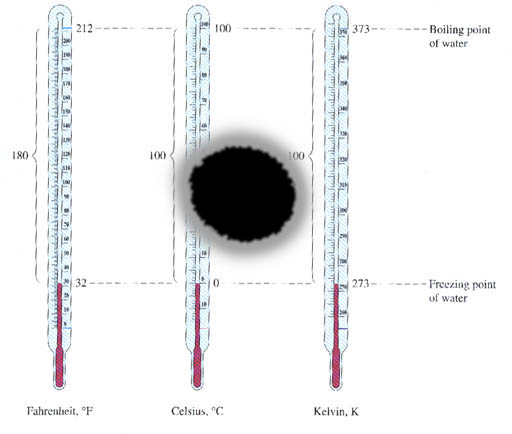
Temperature:
11th Edition, Sec.2.11, p30-32
12th Edition, Sec. 2.8, p33-35
13th Edition, Sec. 2.8, p31-34
Read what the book says about temperature and the three scales used for temperature. Learn how to convert between the three scales. Notice that the book gives you names of the three scales, (Fahrenheit, Celsius, & Kelvin) but does not explain how these names came about or the how the temperature scales were created. I feel that if you don't know this background information, there will always be a hole in your learning. I will cover temperature in a separate tutorial, but if I didn't, you should do your own background check.

Density:
11th Edition, page 35:
12th Edition, page 37
13th Edtion, page 34-37
Density is useful for many aspects of chemistry. It helps you identify
unknown substances. It tells you whether a poisonous gas will rise or
sink which helps you pick the right way to escape. It helps you purify
mixtures and do many more things.
Density can be calculated with simple measurements-volume and mass.
Read Section on Density
The book shows both the algebraic approach and the Dimensional Analysis approach. Trust me, the Dimensional Analysis will be easier in the long run, so focus on that approach. They use parentheses to indicate multiplication, but as I've shown before, a faster way to write it is with vertical lines.
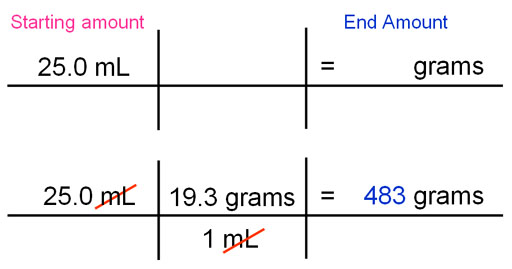
Book Example 2.23:
The density of gold is 19.3g/mL. What is the mass of 25.0 mL of gold?
Here is my suggested style. Write the 25mL as the starting amount and the grams as the end dimensions. The density is given as 19.3 g/mL. These dimensions are good because the grams stays and the mL cancels out the mL in 25.0 mL.
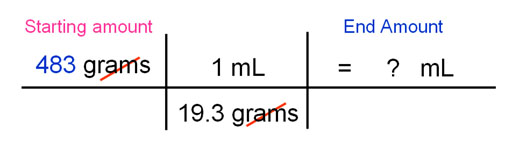
If this problem said, "You have 483 grams of gold. What is the volume?", then the 483 grams would be written first and the density would be written upside down (1 mL/19.3grams) so that the grams cancels out and the mL stays. The answer would be 25.0 mL.

Gold Density Problem 1:
11th Edition, Question 92, page 42
12th Edition: Question 81, page 45
13th Edition: Question 81, page 42
"A gold bullion dealer advertised a bar of pure gold for sale. The gold bar had a mass of 3300g and measured 2.00cm x 15.0cm x 6.00cm. Was the bar pure gold? Show evidence for your answer."
The first part of this problem is to solve for the volume
of the bar. They give you the dimensions of the bar. Realize the volume
of a rectangular solid (a bar) is V=L x W x H (length x width x height).
Use the density of gold mentioned above and dimensional analysis to convert
the volume of the bar into grams. Compare the calculated grams to the
3300 grams that it actually weighed. (a) What should it have weighed if
it were pure gold? (b) Was it pure gold and why? The below spreadsheet helps show the calculation of (1a).
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
|
| 1 | Height x Length x Width = cubic centimeters (cm3) |
Density g/cm3 |
grams if pure gold |
||||||||
| 2 | 2.00 |
cm | 15.0 |
cm | 6.00 |
cm | 19.3 |
g | = |
??? |
grams |
| 3 | 1 |
cm3 | |||||||||

Gold Density Problem 2:
11th Edition, Question 93, page 42
12th Edition: Question 83, page 45
13th Edition: Not in this edition. Problem is shown below.
"The largest nugget of gold on record was found in 1872 in New South Wales, Australia, and had a mass of 93.3 kg.
(2a) Assumming the nugget is pure gold, what is its volume in cubic centimeters?
(2b) What is its worth by today's standards?" (Look up the current value of gold and let me know the value you use for the calculations)
Use dimensional analysis to start with 93.3 kg and
end up with cubic centimeters. Realize that 1 milliliter (mL) is the same
size as a cubic centimeter. Since the density of gold is 19.3 g/mL, you can use 19.3g/cm3 instead. Don't forget
this is 93.3 kilograms not grams, so you will need to get rid of the "kilo".
They give a conversion of 14.58 troy oz = 1 pound.
You will also need to know that 2.2 lbs = 1 kg = 1,000 g. See spreadsheet below for help with layout.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
|
| 1 | Mass of gold nugget |
cancel k |
Density inverted |
(2a) Volume of nugget (cm3) |
|||||||
| 2 | 93.3 |
kg | 1000 |
1 |
cm3 |
= |
??? |
cm3 | |||
| 3 | kilo |
19.3 |
g | ||||||||
| 4 | Notice all units cancel except for cm3. Notice the density of gold (19.3g/cm3) was inverted so that "g" would be in the denomintor so as to cancel the grams in 93.3kg. Also, by inverting the cm3 would be in the numerator and become the answer. | ||||||||||
| 5 | |||||||||||
| 6 | Mass of gold nugget |
convert kg > lbs |
lbs > troy oz |
Current price of gold per troy oz |
(2b)Value of gold nugget |
||||||
| 7 | 93.3 |
kg | 2.2 |
lbs | 14.58 |
troy oz | ??? |
Current $ of gold | = |
??? |
dollars |
| 8 | 1 |
kg | 1 |
lb | 1 |
troy oz | |||||
| 9 | Notice how all units cancel except for dollars (units in red). You need to look up the current price of gold per troy oz. Then you can calculate the dollar value of the gold nugget. The formula for J6 is "=A6*C7*E6". There's no need to divide by the cells that have a "1". | ||||||||||
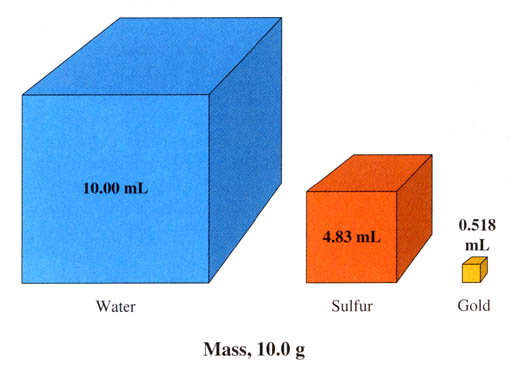
Problem #3: In the textbook they show this graphic to explain density.
What's nice they drew the boxes to scale. In other words, the sulfur box
measured about 1.7 centimeters (cm) on each side. That gives the volume
of 1.7cm x 1.7cm x 1.7cm = 4.9cm3, which is close to the volume
they show for sulfur.
Now look at the large cube for water. It says it holds 10.00 mL of water.
Compare that to the 4.83 mL cube of sulfur. Isn't 10mL about twice as
big as 4.83mL? Does the blue cube look only twice as big? Not really.
The blue cube is about 3.3cm on each side. #3a: In that case what is its
volume?
#3b. To draw a cube that is 10mL, the three sides have to multiply
out to be 10mL. (Remember one cubic centimeter is the same as one mL).
What should have been the size of the sides if they wanted to draw
a 10mL cube? (hint: find the cube root of 10)

Oil Slick Problem example:
11th Edition: Question 52, Page 42
12th Edition: Question 40, Page 44
13th Edition: Question 40, Page 40
Oil spreads in a thin layer on water called an "oil slick." How much area in m2 (square meters) will 200cm3
of oil cover if it forms a layer 0.5nm thick?
This is a bit tricky problem. The slick is considered
a very flat box with a volume equal to L x W x H. Volume is 200cm3(about a cup full).
Height is 0.5nm (about 1/200 of human hair) and the width times the length is the area
Here is the formula and how we solve for area:
V=L x W x H
V = Area x H
V = Area x H
H H
V = Area
H
So if we divide the volume by the height, we get the area. We now can plug in our values.
200cm3= Area
0.5nm
The problem with this is that cubic meters divided by nanometers doesn't give us the square meters were are looking for. We would have to get rid of the centi (c) and the nano (n) first.

With dimensional analysis we put our starting amount on the left (volume divided by height) and what we want to find on the right (area in square meters). Realize that cm3 is cm x cm x cm. cm3 has "m" three times (cubic meter); however, our answer is square meters (m2). The meter in "nm" will cancel one of the meters in the cubic centimeters. Then we end up with the meters squared (m2) that we want. The starting amount also has "centi" (c) three times, so we cancel them by multiplying by 0.01 over "c" three times. Remember "centi=0.01". Then "n" in 0.5nm needs to be canceled so we put "n" on top and its equivalent on the bottom (10-9), which is one billionth).
If dimensions are in the right place, everything that needs to cancel will cancel and you are left with the correct final units (m2). Now we just multiply all of the numerators together and divide by each of the denominators. So the 200cm3, which is less than a cup of oil, can form an oil slick that covers 400,000 m2, which is the area of about 100 football fields!

Problem #4. Here is a picture of the Exxon Valdez. It spilled 11 million gallons of oil. How many square miles of ocean could it cover if the oil also coated the surface also with 0.5nm thickness of oil?
Setup the problem the same as before. We know dividing the volume by the height is the area. However, a volume of gallons divided by a height of nanometers does not give us square miles. We will have to do some conversions. Since our height is in nanometers, it would help to convert gallons to cubic meters. Then both height and volume will be measured in meters. Searching the Web for "metric conversions" we find sites that give us conversions. We find that 1 cubic meter = 264 gallons. Instead of writing "cubic meters", it is better to show "m x m x m" to recognize meters times itself 3 times. At that point we have gotten rid of gallons and have square meters (mxm). Next we need to convert square meters into square miles. We look it up and see that 2,589,988 square meters equals 1 square mile. We use that as the conversion. Finally we need to get rid of the "nano" in "nm". We do that by putting "n" on top and its equivalent "10-9" on the bottom. Problem #4: Do the arithmetic to solve for the square miles. In other words multiply all numerators and divide by each denominator. Hint: The answer will be in millions of square miles. Below I will recreate the last part of the dimensional analysis shown on the left, but use a spreadsheet style layout which gives me some extra ways to organize it.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
|
| 1 | Volume/height=area |
gallons > m3 |
square meters > sq. miles |
|||||||
| 2 | 11000000 |
gallons | 1 |
m3=mxmxm |
1 |
sq. miles |
n |
= |
??? |
sq.miles |
| 3 | 0.5 |
nm | 264 |
gallons |
2589988 |
m2 (sq. meters) |
10-9 |
|||
| 4 | Columns C & D was chosen to cancel the gallons and meters in nm(nanometers). The remaining mxm (sq.meters) is canceled by E & F. Finally the nano in "nm" is canceled with column G. The formula put into a spreadsheet that would calculate the answer is "=A2/A3/C3/E3/G3" | |||||||||
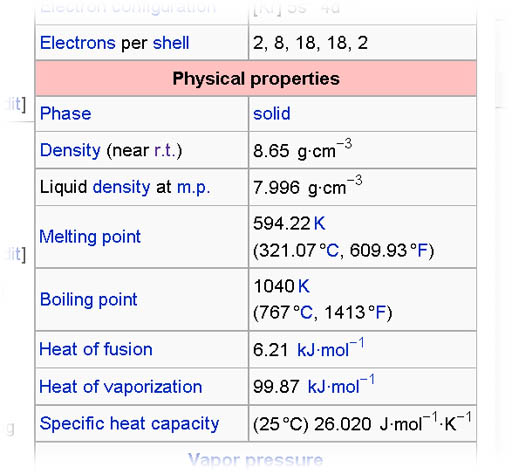
5a) Use wikipedia to search for your element code name.
http://en.wikipedia.org/wiki/Main_Page Once you find the article for your element, look on the right side for table that gives a lot of data. One section of that table is the Physical Properties. In there should be the density of the element. If a gas, it will be given as grams per liter. If solid or liquid, it will be grams per cubic centimeter (abbreviated as g·cm-3or g/cm3). Sometimes they give a range and sometimes they give the melted density. You can just report the density of the solid at room temperature (r.t.). (Don't use the density in the image on the left. That is for cadmium)
5b) Using that density what would a liter (1000 cubic centimeters) weigh? Give answer in grams and in pounds (454 grams = 1 pound)
5c) Water's density is 1 gram per cubic centimeter. Will your element sink or float in water?