 The Galileo thermometer depends on the density differences in the floating spheres and the fact water has slightly different densities at different temperatures.
The Galileo thermometer depends on the density differences in the floating spheres and the fact water has slightly different densities at different temperatures.Discussion: Density is a very useful property. It helps us identify unknown solids, liquids, or gases (See my diamond density example on lab 1 help page). It lets us know what will sink or float. Also, by knowing the density of something, we can figure out its weight if given the volume, or we can figure the volume if given how much it weighs.
Density is also useful because its a fairly easy property to measure. It only requires finding the weight of an object and its volume. You can read about density in this measurement tutorial (density is about half way through the tutorial). Here's the link: http://www.chemistryland.com/CHM130S/02-MMM/Measure/Measuring.htm
 If you see some ice cubes that sink, don't drink it. The bottom ice cubes were made with heavy water, which is water that uses deuterium hydrogen (nucleus with an extra neutron) not regular hydrogen which has no neutron.
If you see some ice cubes that sink, don't drink it. The bottom ice cubes were made with heavy water, which is water that uses deuterium hydrogen (nucleus with an extra neutron) not regular hydrogen which has no neutron.
Objective 1: Learn the definition of density and its usefulness (its applications).
1. Learn the definition of density and its usefulness.
2. Measure the volume of objects using geometry, water displacement, and buoyancy methods.
3. Determine the density of a solid and a liquid using mass/volume. Also, determine density by making a graph of volume versus mass and then finding the slope.

Objective 2: Determine the density of two minerals to aid in their identification.
Many minerals look alike. To tell them apart, one can measure their hardness and their crystal structure. Another way to tell them apart is to find their density.

Objective 3: Determine the density of an archaeological item to help determine its authenticity.
Gold and silver coins are often found in archeological excavations. To determine if these are authentic coins, one needs to see if they are truly made from gold or silver. Find the density of the coin will help determine that.

Objective 4: Determine the density of two liquids to aid in their identification.
The federal Environmental Protection Agency (EPA) and the Arizona Department of Environmental Quality (ADEQ) often investigate the dumping of chemicals (solids and liquids) into the environment. To aid in the identification of the chemical, the density of that chemical is measured.

Objective 5: Explore the lightest (least dense) solid ever made.
Aerogel holds two world records. It is the least dense solid ever made and the world's best heat insulating material. Your kit has a sample of Aerogel granules.

.gif)
Battery charge. The density of the sulfuric acid solution in the battery indicates how charged it is.
The common instrument to measure density of an aqueous (water) solution is with a hydrometer (water+meter). The hydrometer often uses a tube that floats inside of another tube. If density of the water solution is high, then the inner tube will float higher. If the density is low, the inner tube will sink more. The inner tube has markings on it. On the left you read the density marking at the water level. Here it is about 1.035. This means the brownish liquid (beer in this case) is 1.035 times more dense than water. Specific gravity doesn't have units. It is just the ratio of density of the measured liquid to the density of water.
Sulfuric acid in batteries is quite corrosive, so the hydrometers for testing batteries are enclosed (see right image). The sulfuric acid solution is drawn up into the hydrometer using the squeeze bulb at the top. The hydrometer's inner tube will then float to a certain level. The higher it floats, the more dense the acid solution. When a battery is fully charged, the sulfuric acid solution is at its highest density.
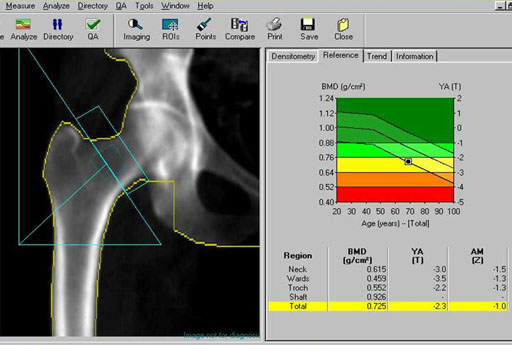
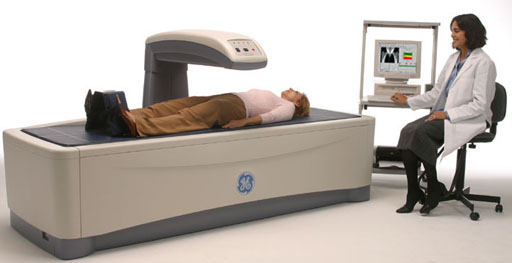
Medical: Bone density is done with a specialized x-ray machine (below). X-rays come up from below the patient and is detected by sensors in the arm over the patient. Bone density relates to bone strength. The condition of osteoporosis (porous bones) exhibits a lower density of the bone and makes bones more prone to breakage.


Urine density can be done using a hydrometer, which uses a floating tube (Left image). The more the inner tube extends above the surface of the urine, the more dense the urine is. The density is read on a scale on the tube. This is the same kind of instrument used to measure the charge of a battery (by measuring sulfuric acid density).
Another way the density of urine is determined is by measuring how much it bends light (refracts light). This is done with refractometers (2 examples are shown). The computer chip in the devices translate the degrees the light bends into density (specific gravity) of the urine. These devices only need a drop of urine to do the testing. A specific gravity above 1.035 indicates a problem.
These devices can also be used with juices and other liquids to determine their density.

Civil and architectural Engineering:
Compaction of soil for roads, dams, and building foundations.
For soil to reach the highest compaction (highest density), it needs water present while it's being compacted. That's why you see water trucks work with the compaction equipment like sheep-foot rollers (shown here).

Astronomy: Density of planets and stars.
The mass of planets and stars are not measured with a balance but by using the force of its gravitational pull. The volume is measured using its diameter and the formula for a sphere. The mass divided by volume gives the density.
Even though Jupiter is mostly gas, it's average density is a little more than the density of water. If it had oceans of water, they would likely be at the core of the planet not on the surface like Earth's oceans. Again, that's because the very high gravity of Jupiter has compressed its atmosphere into a gas more dense than water.
Chemical engineering:
Densities of solids and liquids are exploited to aid in separation and purification of substances. The design of factories are constantly taking into consideration the density of the substances they are manufacturing or using because density is related to the mass of the substances and also dictate what items will sink or float.

Manufacturing:
Density is also used in glass (window) manufacturing. The density of glass is less than that of molten tin. So molten glass will float on top of the molten tin. That makes for very smooth and flat glass, which is required for windows. In the image the glass has left the ovens where it had floated across the tin. (This glass is also called float glass).

Meteorology: Density of air affects the weather and local air pollution.
Normally, air gets colder the higher you go, but if the air is colder near the surface, it can create an "inversion" where cold air is near the surface and warmer (less dense) air is above it. (Usually the cold air is up higher). The dense cold air stays close to the ground and traps smoke and other pollution. The picture is in Scotland, but this effect is commonly seen in Phoenix, Arizona and accounts for the brown cloud that is sometimes seen over Phoenix. Trapped smoke like in the picture is also often seen in Payson, Arizona where a lot of people use fireplaces.


Definition and calculations

1 liter of gold changing to 2 liters of gold causes a change in mass of 42 pounds.
Density tells us how much mass changes when volume changes. If something gets a lot heavier when there's just a small change in volume, then it has a high density. For example with gold, if the change of size goes from 1 liter to 2 liters, the change in size is just 1 liter, however, its mass increased from 19,300 grams to 38,600 grams. So there was a change in mass of 19,300 grams (that's 42 lbs!). So you could express the density as 42 lbs mass change for every 1 liter of volume change. In mathematical language, that's written as a fraction.
42lb
1 Liter
Mixing English units with metric units is not normally done, so we would write
19,300 grams
1 Liter
Since one liter is 1000 cm3 we could write:
19,300 grams
1000 cm3
Density is almost always shown as the mass of one unit of the volume. So the above fraction is reduced by dividing top and bottom by 1000. After reducing we get:
19,300 grams ÷ 1000 = 19.3 grams = 19.3g/cm3
1000 cm3 ÷ 1000 1 cm3
This is the way we normally see it written. The volume is usually just one of whatever the volume is measured in. It is telling us that for every 1 cm3 volume change there will be 19.3 grams of mass change. You can also interpret this as for every 19.3 grams of gold, there will be 1 cm3 volume of gold. This is allows us to find the volume if we know the mass. It also lets us find the mass if we know the volume. So density is very useful.

If you change the volume of Diet Coke from 1 liter to 2 liters, the change of volume is also 1 liter, but the change in mass is only 1000 grams. (2.2 lbs.) So the density is 1000 grams change in mass per 1 liter change in volume, which is the same as 1000 grams per 1000 milliliters (cubic centimeters), which is the same as 1 gram per 1 cubic centimeter (1 cm3).
Density of Diet Coke
1000 g = 1000 g = 1000 g ÷ 1000= 1 gram = 1g/cm3
1 liter 1000 mL 1000 cm3 ÷ 1000 1 cm3
This is the same as water, which makes sense because Diet Coke is essentially just water.
Again, to find density you only need two measurements, volume and mass. In Lab 1 you learned how to find volume and mass, now we just do the division. So what you learned there applies here.
Finding mass is usually straightforward. You simply weigh the object on a balance. Finding volume, as you remember, can be tricky for solid objects.
In math terms it is usually written as d=m/v.
Density is measured in mass per unit volume (unit volume means one liter, mL, cm3, gallon, or some other measurement of volume). So finding density is writing the mass over volume, then reducing it so that volume is just 1.
346 g ÷ 87.4 = 3.96 g and written as 3.96g/mL (the 1 in front of "mL" is understood)
87.4 mL ÷ 87.4 1 mL
Density is usually expressed as grams per 1 cm3 (or 1 mL); however, some literature shows it in kilograms per cubic meter (m3). See below on how to convert kg/m3 into grams per cubic centimeter (cm3). Notice cm3 looks like just meter (m) is cubed, but centi is also cubed, so we need centi multiplied three times. Also, "centi" means one hundredth (0.01), so 0.01 over "centi" is like multiplying by "1".
? kilograms x 1000 x 0.01 x 0.01 x 0.01 = ? grams
m3 kilo centi centi centi cm3
Grams per cubic centimeter can be written as g/cm3, g/cc, g/mL, or g·cm-3.
Notice in the last one, a dot is placed between the "g" and "c"; also, the negative exponent of "-3" means the cm3 is in the denominator. Of course, cc and mL are the same volume as cm3. Also notice that even though usually written as mL or cm3, it really means 1 mL or 1 cm3.
If you know density and mass, you can find volume. Look at the dimensional analysis (label-factor method) below:
19.3 g x 3785mL = 73100 g
1 mL
This density is that of gold (19.3g/mL). When that is multiplied by the volume of gold (1 gallon=3785 mL), it gives us the mass of one gallon of gold. 73,100g is about 161 lbs. Notice that when density is multiplied by volume, the milliliters (mL) cancel out leaving just grams. So using the density of a something times its volume lets you find its mass without actually weighing it. So it's a pretty good trick.

For example, a recipe calls for 1 cup (237 mL) of butter. You really don't want to melt the stick of butter to pour it into a cup; however, you can weigh out the mass of 1 cup of butter with a small balance if you knew how much 1 cup of butter weighs. So you can look up its density in Wikipedia and find that it is 911 grams per liter. Some sources say 0.911 grams per mL, but you realize these densities are the same. Like above, you multiply the density by the volume and you will find mass.
0.911 g x 237mL = 216 g
1 mL
Knowing that one cup of butter weighs 216 grams makes it easy to get the correct amount of butter. You can just slice off butter until you get 216 grams. You don't have to melt it to pour it into a measuring cup.
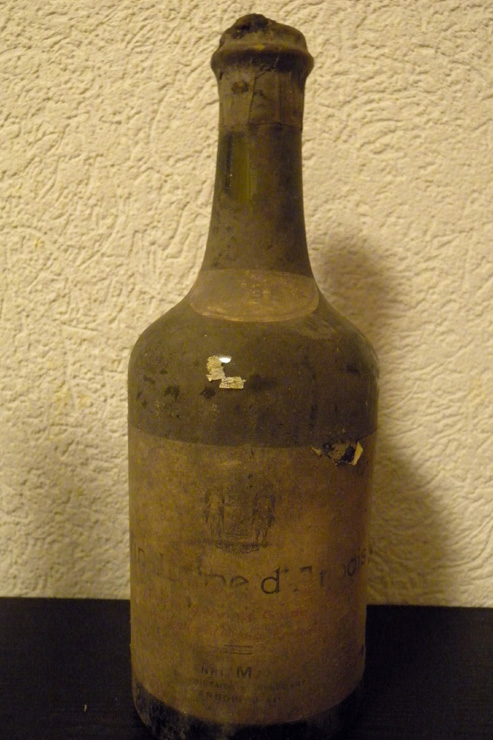
There is also the situation where you need to find the volume of something, but it's not easy or possible to measure the volume directly. So you can use density and mass to calculate volume. For example, a wine collector found what seems to be a rare 100 year old bottle of Royal Vin Jaune wine. An almost identical bottle is found next to it but it was broken and all the wine is gone. To confirm its identity the wine collector needs to know if the volume of the wine in the bottle is 620 mL versus the 750 mL of a standard bottle of wine because only this variety of wine came in bottles that held 620 mL of wine. The density of this variety of wine is known to be 0.968 g/mL. The bottle of wine was weighed and found to be 1129 grams. The broken bottle was 524 grams, which is assumed to be the same kind of bottle. So by subtracting 524 grams from the 1129 grams, we get the mass of just the wine in the bottle. So that's 1129g (wine+bottle)-524g(bottle)=605 grams of wine.
605 g wine x 1 mL = 625 mL
0.968 g
1. Which weighs more, a pound of feathers or a pound of lead?
2. One liter of ice weighs 920 grams. What is its density in grams per mL (cm3)?
3. The density of air room temperature air at 25°C (77°F) is 1.18 grams per liter. The air that you breath out is about 35°C (95°F) and has a density of 1.14 grams per liter. Let's say you breath in one liter of room air. If you exhale that same air, do you breath out one liter of air?
4. Using the data from Problem 3, if you inhale 2 liters of room air, then exhale that same air, how many liters do you breath out?
Hint: 2 liters of room air is 2 x 1.18 grams = 2.36 grams. The density of the air you breath out is 1.14 grams per liter. You can use these two facts to find the volume of what you breath out. The math is like the wine example above.
5. The body of an athlete usually has a density of 1.04 g/cm3 or more. Would an athlete sink or float in water if he or she didn't move or hold their breath?
(answers are at the very end of this page).

These are most of the items you will use for doing density determinations. One of the small jars will be labeled "Lab 3: Minerals".
Again, your kit will either have 4 "gold" coins or 4 "silver" coins. They are stored in one of these small plastic jars.
For density you need to measure mass, so that's why the digital balance is showing. Plus you need to measure volume, which is why the two graduated cylinders are showing.

There are four coins in your kit. They may be a gold color or a silver color. The premise is these coins were found at an archaeological excavation site and suspected to be ancient Spanish gold and silver coins. However, the archeologist thinks they might be just replicas and asking if the metal in these coins are made of silver or gold? Finding their density will help answer that question.
Escudo was the Spanish name for a unit of currency (like our word, dollar). The gold coin here looks like the coin that was worth 2 escudos. The nickname for that coin was "doubloon" (meaning double). You probably heard of the word, doubloon, in pirate movies since a lot of gold treasure was made up of doubloons. You also probably have heard of the gold pieces called "pieces of eight". Those were gold coins worth eight escubos (4 times heavier than the doubloons). The silver coins that your kit may have were worth 2 "reales" (meaning royal). It took 10 reales to make one escudo. So the silver coins were worth 10 times less than their gold coin counterparts.

In theory you could find the density of one coin by weighing it and finding its volume. In practice, however, finding the volume of one coin by water displacement is not very accurate because its small volume doesn't raise the level of the water much in a graduated cylinder. This is why you should find the mass of all four coins and the volume of all four coins as one group. That way the accuracy of volume will be much better.
So first get the weight of the four coins as a group.



After you've gotten a good measurement of the volume of water in the graduated cylinder, drop the 4 coins into 100 mL graduated cylinder. You may want to tilt the graduated cylinder so the coins slide in and not splash water out or up onto the sides of the cylinder.
After placing all 4 coins into the graduated cylinder, get a new reading of the water's volume. By subtracting the previous volume from the new volume, you will have determined the volume of the 4 coins.
Take the mass of the 4 coins (in grams) and divide by the volume in milliliters. That will give you the density of the coins. Remember, the density of all coins is the same as the average density of just one coin.
If your coins are the gold-colored ones, then you are expecting the density to be close to gold, which is 19.3 grams/cm3.
If your coins are the silver-colored ones, then you are expecting the density to be close to silver, which is 10.49 grams/cm3.
What is the density of your coins, and are your coins made from gold or silver?

There are two minerals in your kit where you will use density to help determine their identity. Both are in the small plastic jar labeled "Lab 3: Minerals"
One is a diamond shaped mineral. The other is a gold colored mineral.

Let's start with the one that is diamond shape. First use the balance to get its mass.
To get its volume, we can use a graduated cylinder, and the 10mL graduated cylinder is ten times more accurate than the 100mL graduated cylinder, but this crystal will not fit into the 10mL graduated cylinder, but it will fit into the 100mL graduated cylinder. Unfortunately, the volume of the crystal does not raise the water level in the cylinder enough to get an accurate volume reading. For example, let's say the crystal is about 2 mL, so you might get a volume of 2.3 mL, but that's only 2 significant figures. The mass will be 3 or 4 significant figures. When you divide the mass by the volume, you only get density with 2 sig figs because the answer is limited to the accuracy of the least accurate measurement, which would be the mL measurement.

Here is a technique I designed to improve the accuracy. First fill the 100 mL graduated cylinder about 3/4 full of tap water. Tilt it so that its spout rests on the lip of the 10mL graduated cylinder.


Now use the small beaker to pour water into the 100mL graduated cylinder until some water spills over into the 10 mL graduated cylinder.
Now take an accurate reading of the water level in the 10mL graduated cylinder. (See tip below for getting accurate reading)
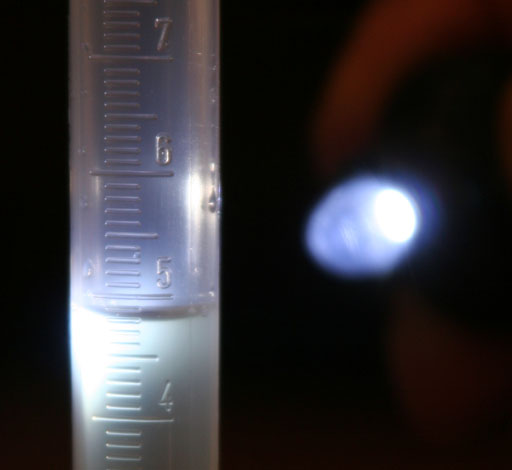

Using the stainless steel microspatula, gently place the diamond shaped crystal into the 100 mL graduated cylinder. This will displace water in the 100mL graduated cylinder, which will spill over into the 10mL graduated cylinder. The volume of the crystal will equal to the amount of water that spills over. Now read the new level in the 10mL graduated cylinder. Subtract the previous level in the 10 mL graduated cylinder and that's the volume of the crystal.
To be more confident, you may want to measure volume again by repeating the above steps.
Divide mass of the crystal by its volume to get its density. What is the crystal's density?
Here are some minerals which are being considered. Use your density to choose which one of these is consistent with your density measurement:
Quartz: 2.7 g/cm3
Kyanite: 3.6 g/cm3
Fluorite: 3.3 g/cm3
Beryl: 2.7 g/cm3

The other mineral in "Lab 3: Minerals" jar is gold in color. You may have one piece or several pieces including small grains.


In this example, the gold colored mineral had broken up into small pieces. So all of these mineral pieces were weighed together.
Be careful to note if the mass that is displaying is just of the minerals or of the minerals plus the watch glass. If you tared the watch glass, then the mass will just be of the minerals. If not, you will have to subtract the mass of the watch glass to know the mass of the minerals.

To find the volume these gold colored pieces, you will do the same thing as you did for the first crystal. Fill the tilted 100mL graduated cylinder until it spills over into the 10 mL cylinder.




Then pour the small pieces into the 100 mL graduated cylinder. If a few small pieces fall into the 10 mL graduated cylinder, that's fine too. Matter of fact, you could just pour these small pieces directly into the small 10 mL graduated cylinder. That's because either way, the water level in the small 10 mL graduated cylinder will go up by the volume of these pieces.
Now get an accurate reading of the new level in the 10 mL graduated cylinder.
If you don't feel confident about your volume measurement, you can repeat the process to see if it's close to the first time you did it.
What is the gold-colored mineral's density?
Here are some minerals which are being considered. Use your density to choose which one of these below is most consistent with your density measurement:
Galena: 7.5 g/cm3
Pyrite: 5.0 g/cm3
Sphalerite: 3.9 g/cm3


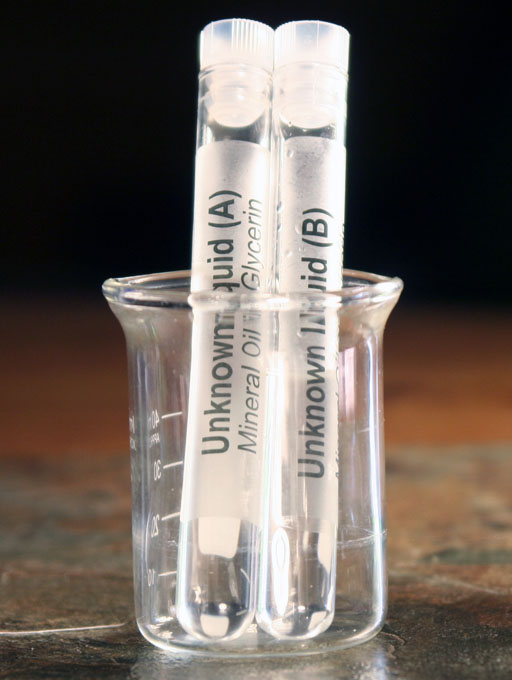
Your kit has 2 test tubes labeled Unknown "A" and Unknown "B". One is mineral oil and the other is glycerin. You will use density to see which is which.
Take the 2 test tubes from the test tube holder in the kit and place them in the small 50 mL beaker. The beaker is a handy item for holding a few test tubes.

When you have a situation where you have some empty containers that match the containers holding items of interest, there are some shortcuts that you can take advantage of. For example, one shortcut is that you do not have to remove these liquids to weigh them.
The kit has some empty test tubes that have the same caps as the two test tubes that hold the unknown liquids. You will use one of them to cancel the mass of the test tubes with the unknown liquids.

First prove to yourself that the 3 empty test tubes in your kit with the clear plastic caps have masses that are close to each other. Put the small beaker on the digital balance and press TARE. That will, of course, zero out the mass of the beaker. Now place one of the empty test tubes with its cap on in the beaker and note the mass. Now take that test tube out and do the same with the second empty test tube. Check its mass. Now do the same thing for the third test tube. Note how close they are. You will see that they are less than a tenth of gram apart. We can assume the test tubes that hold the unknown A and B have close to the same mass as these test tubes.
Again put the small beaker on the digital balance and press TARE to zero out its mass. Now place one of the empty test tubes with its cap in the small beaker. Press TARE again. That will zero out the mass of the test tube. Now take out the test tube. Notice that the display on the balance will show the mass of the test tube as a negative number.
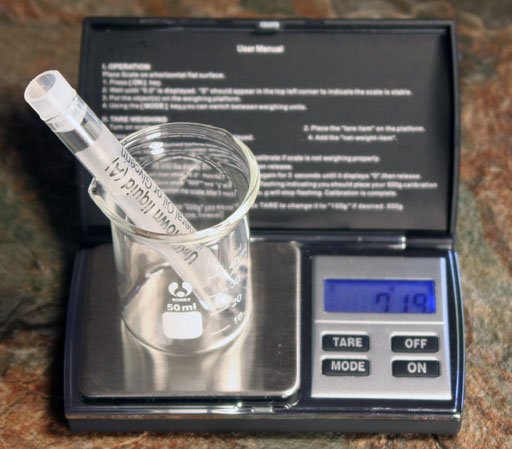
Now place the test tube with Unknown liquid "A" into the beaker. The mass of the test tube holding the liquid will bring the mass up to zero and the mass of the liquid will be the only mass displayed. In other words, the balance is set so that the mass of the beaker and the mass of a test tube and cap is zero. So that mass does not show up when you measure the test tube with the unknown liquid. In essence, you find the mass of the liquid without taking it out of the test tube. If you swap in Unknown "B" into the beaker (before the balance shuts itself off), you will see the mass of the Unknown liquid "B". Now you have the mass of the liquids, so next you need their volumes in order to find their densities. Again, we can do it without taking the liquids out of their test tubes.
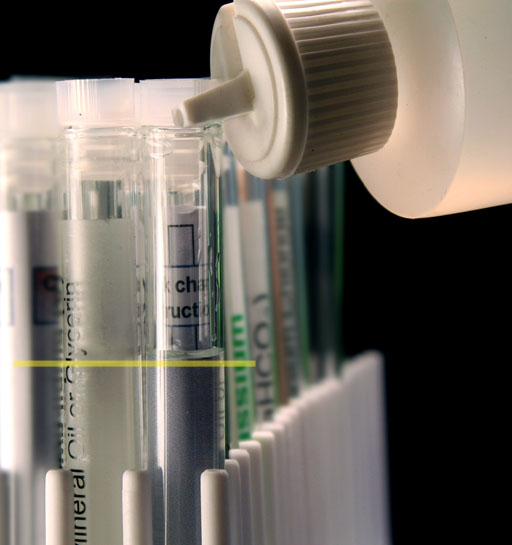
Remove the test tube rack from your kit and put the Unknown "A" test tube next to an empty test tube. Use your bottle with purified water to fill the empty test tube up to the same height (same volume) as the liquid in Unknown "A" test tube.
Instead of finding the volume of the water you added by pouring into a graduated cylinder, we will find the volume by weighing the water.

A quick way to weigh the water is to use the same trick as before. Place an empty test tube into a beaker and press the TARE button to zero out the weight of beaker and test tube.

Now take the empty test tube out of the beaker and replace it with the test tube that you added water to match the height of the liquid in Unknown "A". The balance will give you the mass of just the water.
At room temperature, the density of water is 0.997 grams per 1 mL. If you round to two significant figures, which is OK for this check of density, the density of water is 1.0 grams per 1 mL. In the photo, the water weighs 5.75 grams. We can then do the below math by using the invert of the density.
1 mL x 5.75 grams = 5.75 mL
1.0 gram
The 5.75 mL should be rounded to 2 sig figs to make 5.8mL.
When using water, weighing it is a quick way to also find its volume. If you wanted 3 sig figs, just use the 0.997 g/mL:
1 mL x 5.75 grams = 5.77 mL
0.997 grams

Now that you have the mass and volume of Unknown "A", you can calculate its density. Just divide the mass of the liquid in Unknown "A" by its volume. Use Wikipedia or some other source on the Internet to find the density of mineral oil and glycerin in grams per mL (or cm3). Using your calculated value of Unknown "A", decide if it is mineral oil or glycerin.
Do the same thing as you did with Unknown liquid "A" but with Unknown liquid "B". Find its mass and volume, which will let you calculate its density.

A lab about density isn't complete without a look at Aerogel, which holds two records. It is the lightest (least dense) solid ever made and the world's best heat insulating material.
Find the Aerogel in the kit and shake it back and forth. You will not be able to feel any mass as it hits both ends of the test tubes. If you do that with other test tubes in the kit, you will feel the mass of the powder being shaken from end to end.
Finding density of Aerogel is a little harder because if you open the cap, the Aerogel will immediately start absorbing water from the air making it heavier by the minute. So the best way to measure density would be to do it the same way as the liquids above; however, you've done that, so let's explore some other interesting properties of Aerogel.

If a block of Aerogel like the one shown was sealed in light-weight plastic and the air pumped out of the Aerogel, it would be lighter than air and just float away. That also means a block of Aerogel the size of a house could be wrapped in plastic and hooked up to a vacuum pump to evacuated all of the air. At that point the house sized Aerogel would just float away.

Aerogel is quite strong despite the fact it is so light.
Here a 2 gram (weight of a dime) block of Aerogel is holding up this heavy brick. So the house size block of Aerogel mentioned above is strong enough to hold up a real house, yet light enough to float like a helium balloon.
Now let's learn more about its insulating properties.

This photo shows the incredible insulating property of Aerogel. A quarter inch slice of Aerogel will keep this flower cool even though a 2,000°F flame is 1/4 inch away. That is why Aerogel is used as as tile under the Space Shuttle to protect it from the heat of re-entering the atmosphere. It is light weight and a great insulator making it perfect for items placed in space. However, there is another subtle property of Aerogel. Notice that is has a light blue color.
Aerogel is made of quartz, which is crystal clear, so why is it look blue? The answer is the same answer that explains why the sky is blue.
The sky is blue because the air molecules (nitrogen and oxygen) scatter light of high frequencies (the bluish colors). Aerogel has extremely small interconnected chains of silicon dioxide (quartz). The chains of silicon and oxygen atoms are small enough to scatter the blue light. The yellow end of the light spectrum is not scattered as much so continues straight ahead. That is why the sun looks yellow, when it is actually white.

Locate the keychain flash light in your kit. Its on the right side of the back panel and only the chrome ring is showing.
Note, your keychain flash light might look different.

Turn on the keychain light and take off the cap to the test tube with the Aerogel. Place the light so that it shines into the Aerogel.
You ought to see that the top of the Aerogel is blue. A darker background helps show this.
Now if you hold the test tube higher and look up from the bottom of the test tube, it should look yellow. This shows the Aerogel is scattering the blue light just like the sky and letting the yellow end of the light spectrum go straight through.
Report what you see.
Don't forget to place the cap back onto the Aerogel test tube so that it doesn't absorb water from the air.
If you wish, you can copy the below summary into your email (or Word document) and type your answers after the descriptions. The required photos can either be attached to the email or inserted in the Word document if going that route. Try to keep each image under 2 megabytes. If the first letter of your last name is between A and G, send your lab reports to Loree Cantrell-Briggs at Loree.Cantrell-Briggs@phoenixcollege.edu If the first letter of your last name is between H and Z, send your lab reports to Quinn Thacker at QRT2004@yahoo.com. Be sure to title the email "Lab 3".
A. Spanish coins:
1. Did your kit have silver or gold Spanish coins?:
(Attach photo of the coins on the digital balance)
2. Mass of the 4 ancient Spanish coins:
3. Initial volume of the water in the graduated cylinder:
4. Volume of the water in the graduated cylinder after the 4 coins were added:
5. Volume increase is also volume of the 4 coins:
6. Divide mass by volume to get density of the coins:
7.Silver has density of 10.49 g/cm3. If your kit had silver coins, were your coins made of real silver?
8. Gold has density of 19.3 g/cm3. If your kit had gold coins, were your coins made of real gold?
B. Diamond shaped mineral:
1. Mass of the diamond shaped mineral:
(Attach photo of your setup with the 100 mL graduated cylinder leaning on the 10 mL graduated cylinder with your face also showing.)
2. Initial volume of the water in the 10 mL graduated cylinder:
3. Volume of the water in the 10 mL graduated cylinder after the diamond shaped mineral was added to the 100 mL graduated cylinder.
4. Volume increase in the 10 mL graduated cylinder is also the volume of the mineral:
5. Divide this mineral's mass by volume to get its density:
6. Which of the four minerals listed is the best match for the density you found?
C. Gold colored mineral:
1. Mass of the gold colored mineral:
2. Initial volume of the water in the 10 mL graduated cylinder:
3. Volume of the water in the 10 mL graduated cylinder after the gold colored mineral piece (or pieces) were added to the 100 mL graduated cylinder:
4. Volume increase in the 10 mL graduated cylinder is also the volume of the mineral:
5. Divide this minerals’ mass by volume to get its density:
6. Which of the three minerals listed is the best match for the density you found?
D. Unknown Liquid A:
1. Mass of the liquid in Unknown "A" test tube:
2. Volume of the unknown liquid "A" estimated to the nearest 0.1 mL:
3. Density of Liquid A (mass divided by volume) to 2 significant figures:
E. Unknown Liquid B:
1. Mass of the liquid in Unknown "B" test tube:
2. Volume of the unknown liquid "B" estimated to the nearest 0.1 mL:
3. Density of Liquid B (mass divided by volume) to 2 significant figures:
4. Use the Internet to find the density of mineral oil and the density of glycerin. What did you find as their densities?
5. Is Unknown Liquid A mineral oil or glycerin?
6. Is Unknown Liquid B mineral oil or glycerin?
F. Aerogel: The lightest (least dense) solid ever made
1. Report what you saw when you shined the light through the Aerogel.
Post-Lab questions and problems are on the Sapling Learning website. Those are graded automatically, so you will get your score on your Post-lab questions as soon as you finish them. http://www2.saplinglearning.com/
1. Which weighs more, a pound of feathers or a pound of lead?
3. The density of air room temperature air at 25°C (77°F) is 1.18 grams per liter. The air that you breath out is about 35°C (95°F) and has a density of 1.14 grams per liter. Let's say you breath in one liter of room air. If you exhale that same air, do you breath out one liter of air?
Hint: 2 liters of room air is 2 x 1.18 grams = 2.36 grams. The density of the air you breath out is 1.14 grams per liter. You can use these two facts to find the volume of what you breath out. The math is like the wine example above.
There is more than one way to solve this but using the approach we did with the wine bottle problem, we take the grams and multiply by the density inverted. The grams of room air that was inhaled was 2.36 grams. If we multiply that by the warm exhaled air density inverted, we get volume.
2.36 grams x 1 liter = 2.07 liters of warm exhaled air.
1.14 g
Inverting the density of the warm air puts grams in the denominator, which cancels the grams in 2.36 grams leaving just liters of warm air.